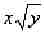Using the Stack


Description

In order to perform operations in RPN mode, the object or objects must be placed on the stack. Entries on the stack are numbered and each entry on the stack has an associated level (the number of the line on which the entry appears). This document discusses placing, entering, and retrieving objects on the stack. This document also gives examples of stack calculations.
NOTE: To use the stack, the calculator must be in RPN mode. To activate the RPN mode, press MODE to access the CALCULATOR MODES input form, and set the mode option to RPN.
Back to top

Calculator symbol key

The procedures in this document use the following text to represent symbol keys:
KeyDescriptionText representation
Right shift key RS
Left-shift key LS
Move cursor left cursor-left
Move cursor right cursor-right
Move cursor up cursor-up
Move cursor down cursor-down
X root of y XROOT
Divide divide
Back to top

Placing objects on the stack

New objects can be created and placed on the stack or objects can be retrieved from the calculator's memory and placed on the stack.
Back to top

Entering a number on the stack

To enter a number on the stack, do the following:
  1. Use the NUMERIC keys to enter the number.
  2. Press ENTER (the number will appear on level 1 of the stack).
Back to top

Entering an object that was created in an application, such as a matrix or an equation

To enter an object that was created in an application, such as a matrix or an equation, do the following:
  1. Access the MATRIX WRITER or EQUATION WRITER.
  2. Create the matrix or equation.
  3. Press ENTER to place the matrix or equation on level 1 of the stack.
Back to top

Retrieving an object from memory and placing it on the stack

To retrieve an object from memory and place it on the stack, do the following:
  1. Press VAR to display the directories and variables in the current directory.
  2. Navigate to the directory that holds the desired object.
  3. Press the appropriate function key to select the object.
    NOTE: When a new item is added to the stack, the existing items are pushed up a level. That is, the item at level 1 is pushed up to level 2, and the item at level 2 is pushed up to level 3, and so on.
Back to top

Example of stack calculations

One-argument commands

To use a one-argument command, do the following:
  1. If the argument is not already on level 1 of the stack, enter the argument onto the command line (and, optionally, onto the stack). If the argument is already on level 1 of the stack, go directly to Step 2.
  2. Execute the command by pressing ENTER.

Example of using a one argument command

To calculate 1/sin 30, do the following:
  1. Enter 30, then press ENTER.
  2. Press SIN. (The result of sin 30 is now on level 1 of the stack. This result can be used as the argument of a further command without having to re-enter the result.)
  3. Press 1/x.
    NOTE: If the answer is symbolic when a numeric answer was wanted, press LS+NUM.
Back to top

Using multi-argument commands

Method 1

To use method 1 in using multi-argument commands, do the following:
  1. Enter the arguments, pressing ENTER after each one.
  2. Execute the command.

Method 1 example of executing multi-argument commands

To calculate 23 x 97, do the following:
  1. Enter 23 and press ENTER.
  2. Enter 97 and press ENTER (23 is now on level 2 of the stack and 97 is on level 1).
  3. Press x.
In this example, the order in which the arguments are entered does not affect the answer. However, this is not always the case with two-argument commands. For example, 52 raised to the power of 3 is different from 3 raised to the power of 52. Therefore, 52 must be entered before 3 in order to get the correct answer. Other examples where the order in which the arguments are entered affects the answer include the following:
  • Subtraction
  • Division
  • Percentage commands (%, %CH, and %T)

Method 2

In method 1, each argument is entered onto its own level of the stack before the command is executed. Another way is to enter all of the elements onto the command line separating each with a space. You can then do either of the following:
  • Press ENTER to place the arguments onto the stack and then execute the command.
  • Execute the command with the arguments still on the command line.

Method 2 example of using multi-argument commands

To calculate the cube root of 531441, do the following:
  1. Enter 531441, SPC, then 3
  2. Press ENTER
  3. Press LS, then XROOT
Back to top

Multi-command calculations

Because the result of a calculation is retained on the stack, complex calculations can be easily performed by accumulating the results of sub-calculations on the stack and then treating the results as the arguments in further calculations.

Example of multi-command calculations

To calculate 132 -(17 x 19) + 3/7, do the following:
  1. Enter 132, LS, then x (the result, 169, appears on level 1 of the stack).
  2. Enter 17 and press ENTER
  3. Enter 19 and press ENTER
  4. Press x (the product of 17 and 19, which is 323, appears on level 1 of the stack, and the previous result, 169, appears on level 2).
  5. Press [ - ]
  6. Press 3, ENTER, 7, then divide to place the result of 3/7 on level 1 of the stack.
  7. Press + to add this to the previous result.
    NOTE: If the calculator is in exact mode, the result appears as a number and a fraction. To display the approximate answer to 12-digit accuracy, press LS+NUM.

Example of using computer algebra commands

To substitute x=y + 3 in x2+ 3x +7, do the following:
  1. Use the EQUATION WRITER to create2x + 3x + 7 and press ENTER to place it on level 1 of the stack.
  2. Use the EQUATION WRITER to create the substitution x=y+3, and press ENTER.
  3. Press LS, then ALG to access the ALGEBRA COMMAND menu and select the SUBST command. The HP 49g performs the substitution and the result appears on level 1 of the stack.
Back to top