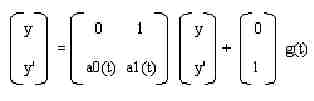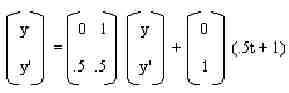Introduction
The
calculator has the capability of solving an initial value second order
differential equation. Below is information on this process with the
appropriate keystrokes. It is important to note that the equation must
be linear with respect to y and its derivatives. Something such as
y'=e^y is not possible because, for the e^y term, y is not linear.
Solving a vector-valued differential equation
Vector-valued equations can be used to solve second-order (or higher) differential equations given two or more initial values.
Another way to write the following second-order equation is shown below (see Figure 1):
y'' =a1(t)y' + a0(t)y + g(t)
Next substitute w for the vector [y y'], fw for the 2X2 matrix, and c for [0 1], which yields the following:
w' = fw*w + c*g(t)
This is a first-order differential equation.
Example
Solve the following equation for w(1) given that y(0)=0 and y'(0)=0 (or w(0)=[0 0])
y" = .5y' + .5y + .5t + 1
Step 1: Convert the equation into a first-order equation (see Figure 2):
Step 2: Store the values in the variables fw:
and c:
[ 0 1 ].
To do this, enter the 2X2 matrix (see Figure 3) above onto the stack and store it into a variable named fw. Similarly, put the vector [0 1] on the stack and store it into variable c.
Step 3: Enter the equation and initial values, set the solution variable to w, and solve for w(1):
- Bring up the differential equation solver and store fw*w+c*(0.5*t+1).
- Make the independent variable T and the soln variable W.
- Set your initial values to zero (because y (0)=0 is a given point).
- Put 1 into the final value of T (because we are solving for w(1)).
When
you solve for final W you should get [0.718262064225 1.71826206422] as
your answer. The first value is y(1) and the second value is y'(1).